Pembahasan Penalaran Matematika

Pembahasan :

Langkah pertama: Hitung perkiraan banyak telur yang dapat dikumpulkan dari ayam pada kelompok 1 dalam 12 hari.

Telur ayam pada kelompok 1 diambil setiap 3 hari sekali dan rata-rata dapat dikumpulkan 100 butir telur dalam sekali pengambilan. Oleh karena itu, dalam 12 hari, telur ayam pada kelompok 1 diambil sebanyak 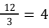 kali. Dengan demikian, perkiraan banyak telur yang dapat dikumpulkan adalah 100 × 4 = 400 butir telur.

Langkah kedua: Hitung perkiraan banyak telur yang dapat dikumpulkan dari ayam pada kelompok 2 dalam 12 hari.

Telur ayam pada kelompok 2 diambil setiap 4 hari sekali dan rata-rata dapat dikumpulkan 150 butir telur dalam sekali pengambilan. Oleh karena itu, dalam 12 hari, telur ayam pada kelompok 2 diambil sebanyak 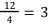 kali. Dengan demikian, perkiraan banyak telur yang dapat dikumpulkan adalah 150 × 3 = 450 butir telur.

Langkah ketiga: Hitung perkiraan banyak telur yang dapat dikumpulkan dari ayam pada kelompok 3 dalam 12 hari.

Telur ayam pada kelompok 3 diambil setiap 6 hari sekali dan rata-rata dapat dikumpulkan 225 butir telur dalam sekali pengambilan. Oleh karena itu, dalam 12 hari, telur ayam pada kelompok 3 diambil sebanyak 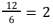 kali. Dengan demikian, perkiraan banyak telur yang dapat dikumpulkan adalah 225 × 2 = 450 butir telur.

Langkah keempat: Hitung perkiraan banyak telur yang dapat dikumpulkan dari ayam pada ketiga kelompok dalam 12 hari.

Dalam 12 hari, perkiraan banyak telur yang dapat dikumpulkan dari kelompok 1, 2, dan 3 secara berurutan adalah 400, 450, dan 450 butir telur. Dengan demikian, perkiraan banyak telur yang dapat dikumpulkan dari ayam pada ketiga kelompok dalam 12 hari adalah 400 + 450 + 450 = 1. 300 butir telur.

Analisis pilihan jawaban yang salah

• Pilihan jawaban A, yaitu 2.250, bukan merupakan pilihan jawaban yang tepat. Kesalahan utama dalam perhitungan terjadi saat menghitung perkiraan banyak telur yang dapat dikumpulkan dari ayam pada masing-masing kelompok yang seharusnya mengalikan banyak telur yang dikumpulkan dalam sekali pengumpulan dengan banyak pengambilan, tetapi justru mengalikan banyak telur yang dikumpulkan dalam sekali pengumpulan dengan durasi jeda antar pengambilan telur, yaitu 100 × 3 + 150 × 4 + 225 × 6 = 2. 250.
• Pilihan jawaban C, yaitu 950, bukan merupakan pilihan jawaban yang tepat. Kesalahan utama dalam perhitungan adalah menganggap bahwa telur diambil sebanyak 2 kali saja (didapat dari 12 hari yang dibagi dengan jeda waktu terlama antar pengambilan telur, yaitu 6 hari). Oleh karena itu, perhitungannya justru menjadi 2 × (100 + 150 + 225) = 950.
• Pilihan jawaban D, yaitu 825, bukan merupakan pilihan jawaban yang tepat. Kesalahan utama dalam perhitungan adalah dengan menganggap tidak ada pengambilan telur di hari ke-12 sehingga banyak pengambilan telur dari masing-masing kelompok berkurang 1. Banyak pengambilan telur di kelompok 1 menjadi 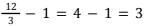 kali, banyak pengambilan telur di kelompok 2 menjadi  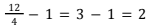kali, dan banyak pengambilan telur di kelompok 3 menjadi  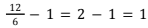kali. Oleh karena itu, perhitungannya justru menjadi 100 × 3 + 150 × 2 + 225 × 1 = 825.
• Pilihan jawaban E, yaitu 475, bukan merupakan pilihan jawaban yang tepat. Kesalahan utama dalam perhitungan adalah menganggap bahwa telur diambil sebanyak 1 kali saja. Oleh karena itu, perhitungannya justru menjadi 100 + 150 + 225 = 475.

Jadi, jawaban yang tepat adalah B.

Pembahasan :

Diketahui lantai aula berbentuk persegi yang akan dipasangi keramik-keramik berwarna putih dan hitam. Berdasarkan gambar, pola pertama memiliki dimensi ukuran 2 × 2, pola kedua 4 × 4, dan seterusnya.

Berdasarkan informasi pada soal, dapat diperhatikan bahwa untuk aula berdimensi n × n, banyak keramik putih akan mengikuti rumus berikut.

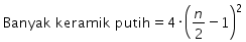
Jika banyak keramik putih adalah 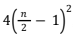, maka banyak keramik hitamnya adalah total keramik dikurang banyak keramik putih, yakni

Diketahui perbandingan banyak keramik putih dan hitam 81: 19. Akibatnya, akan diperoleh perhitungan berikut.

Diperoleh 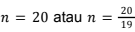, tetapi karena n menyatakan banyaknya keramik, maka nilai n harus bernilai bulat. Oleh karena itu, diperoleh nilai n yang memenuhi adalah n = 20.

Dengan demikian, total banyak keramik (hitam dan putih) di aula tersebut adalah 

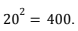
Jadi, jawaban yang tepat adalah C.

Pembahasan:

Diketahui bahwa barang A seberat 1.450 g barang B seberat 0,5 kg = 500 g dan barang C seberat 3,2 g = 3.200 g.

Diketahui pula terdapat penambahan biaya pengemasan sebesar Rp3.000,00 untuk setiap pengiriman.

Untuk mengetahui total biaya termurah yang dikeluarkan oleh Anggun, akan diperiksa biaya yang dikeluarkan untuk setiap kemungkinan berikut.

Kemungkinan 1: Pengiriman barang A dan B digabung, sedangkan barang C terpisah.

Karena barang A digabung dengan barang B, maka beratnya menjadi 1.450g + 500g = 1.950g. Total biaya yang dikeluarkan adalah sebagai berikut.

Total biaya

= Biaya barang A dan B + biaya barang C + 2 x biaya pengemasan

= 13.250 + 13.250 + 3.000 x 2

= 26.500 + 6.000

= 32.500

Didapat bahwa biaya yang dikeluarkan Anggun pada kemungkinan 2 adalah Rp 32.500,00.

Kemungkinan 2: Pengiriman barang A dan C digabung, sedangkan barang B terpisah.

Karena barang A digabung dengan barang C, maka beratnya menjadi 1.450g + 3.200g = 4.650g. Total biaya yang dikeluarkan adalah sebagai berikut.

Total biaya

= Biaya barang A dan C + biaya barang B + 2 x biaya pengemasan

= 24.500 + 6.900 + 3.000 x 2

= 31.400 + 6.000

= 37.400

Didapat bahwa biaya yang dikeluarkan Anggun pada kemungkinan 1 adalah Rp37.400,00.

Kemungkinan 3: Pengiriman barang B dan C digabung, sedangkan barang A terpisah.

Karena barang B digabung dengan barang C, maka beratnya menjadi 500g + 3.200g = 3.700g. Total biaya yang dikeluarkan adalah sebagai berikut.

Total biaya

= Biaya barang B dan C + biaya barang A + 2 x biaya pengemasan

= 24.500 + 13.250 + 3000 x 2

= 37.750 + 6.000

= 43.750

Didapat bahwa biaya yang dikeluarkan Anggun pada kemungkinan 3 adalah Rp 43.750,00.

Berdasarkan ketiga kemungkinan tersebut, biaya termurah yang dikeluarkan Anggun adalah Rp32.500,00.

Jadi, jawaban yang benar adalah D.

Pembahasan:

Diketahui bahwa barang A seberat 1.450 g barang B seberat 0,5 kg = 500 g dan barang C seberat 3,2 g = 3.200 g.

Untuk mengetahui pilihan yang paling tidak menguntungkan, akan diperiksa biaya yang dikeluarkan pada setiap pilihan jawaban yang diberikan.

Pilihan jawaban A: Pengiriman barang A, B, dan C digabung.

Karena semua barang digabung, maka beratnya menjadi 1.450g + 500g + 3.200g = 5.150g. Kemudian, total biaya yang dikeluarkan adalah sebagai berikut.

Total biaya

= Biaya gabungan barang A, B, dan C + biaya pengemasan

= 37.700 + 3.000

= 40.700

Didapat bahwa biaya pengiriman pada pilihan A adalah Rp40.700,00.

Pilihan jawaban B: Pengiriman barang A, B, dan C masing-masing terpisah.

Karena ketiga barang dikirim terpisah, maka total biaya yang dikeluarkan adalah sebagai berikut.

Total biaya

= biaya barang A + biaya barang B + biaya barang C + 3 x biaya pengemasan

= 13.250 + 6.900 + 13.250 + 3000 x 3

= 33.400 + 9.000

= 42.400

Didapat bahwa biaya pengiriman pada pilihan B adalah Rp42.400,00.

Pilihan jawaban C: Pengiriman barang A dan C digabung, sedangkan barang B terpisah.

Karena barang A digabung dengan barang C, maka beratnya menjadi 1.450g + 3.200g = 4.650g. Kemudian, total biaya yang dikeluarkan adalah sebagai berikut.

Total biaya

= biaya barang A dan C + biaya barang B + 2 x biaya pengemasan

= 24.500 + 6.900 + 3000 x 2

= 31.400 + 6.000

= 37.400

Didapat bahwa biaya pengiriman pada pilihan C adalah Rp37.400,00.

Pilihan jawaban D: Pengiriman barang A dan B digabung, sedangkan barang C terpisah.

Karena barang A digabung dengan barang B, maka beratnya menjadi 1.450g + 500g = 1.950g. Kemudian, total biaya yang dikeluarkan adalah sebagai berikut.

Total biaya

= biaya barang A dan B + biaya barang C + 2 x biaya pengemasan

= 13.250 + 13.250 + 3000 x 2

= 26.500 + 6.000

= 32.500

Didapat bahwa biaya pengiriman pada pilihan D adalah Rp32.500,00.

Pilihan jawaban E: Pengiriman barang B dan C digabung, sedangkan barang A terpisah. 

Karena barang B digabung dengan barang C, maka beratnya menjadi 500g + 3.200g = 3.700g.  Kemudian, total biaya yang dikeluarkan adalah sebagai berikut.

Total biaya

= biaya barang B dan C + biaya barang A + 2 x biaya pengemasan

= 24.500 + 13.250 + 3000 x 2

= 37.750 + 6.000

= 43.750

Didapat bahwa biaya pengiriman pada pilihan E adalah Rp43.750,00.

Berdasarkan perhitungan tersebut, biaya yang paling mahal adalah Rp43.750,00.

Dengan demikian, pilihan yang paling tidak menguntungkan bagi Anggun adalah pengiriman barang B dan C digabung, sedangkan barang A terpisah.

Jadi, jawaban yang benar adalah E.

Pembahasan:

Misalkan penghasilan Nisa selama 1 tahun adalah P, maka besarnya dalam setahun yaitu sebagai berikut.

P = Rp 42.500.000,00 x 12

P = Rp 510.000.000,00

Misalkan penghasilan kena pajak Nisa sebesar 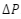, maka karena Nisa belum menikah dan tidak memiliki tanggungan, PTKPnya sebesar Rp54.000.000,00, sehingga besarnya penghasilan Nisa yang kena pajak yaitu sebagai berikut.

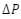 = P – 54.000.000,00

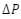 = 510.000.000, 00 – 54.000.000,00

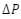 = 456.000.000,00

Dengan membandingkan 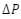 dengan tabel yang diberikan dalam soal, maka penghasilan kena pajak Nisa akan dikenakan tarif progresif sebesar 25%.

Jadi, jawaban yang benar adalah C.

Pembahasan:

Segitiga yang dimaksud memiliki kriteria sebagai berikut.

• Salah satu sisi adalah garis tinggi.

• Salah satu garis bagi adalah garis berat.

Garis tinggi adalah garis tegak lurus yang menghubungkan salah satu titik sudut segitiga ke salah satu sisi segitiga.

Diketahui salah satu sisi merupakan garis tinggi. Akibatnya, terdapat dua sisi segitiga yang saling tegak lurus. Segitiga dengan kriteria ini adalah segitiga siku-siku.

Kemudian, diketahui salah satu garis bagi juga berperan sebagai garis berat. Garis bagi membagi sudut sama besar, sedangkan garis berat membagi sisi sama panjang.

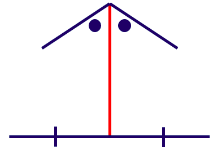
Kesimpulan sebelumnya menyatakan bahwa segitiga yang dimaksud merupakan segitiga siku-siku. Sudut siku-siku yang mungkin adalah sudut yang dibagi oleh garis bagi yang ditandai warna merah.

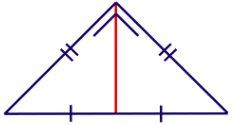
Dengan demikian, segitiga yang dimaksud adalah segitiga siku-siku sama kaki.

Jadi, jawaban yang benar adalah A.

Pembahasan:

Berdasarkan informasi pada soal, kategori penduduk tidak produktif meliputi kelompok usia di bawah 15 tahun dan 60 tahun ke atas. Oleh karena itu, jumlah penduduk dari kedua kelompok usia tersebut adalah sebagai berikut.

n (tidak produktif) = 65 + 24

                               = 89

Sementara itu, jumlah seluruh penduduk di negara tersebut adalah sebagai berikut.

n (total) = 65 + 66 + 62 + 48 +24

              = 265

Persentase penduduk dengan kategori usia tidak produktif dapat dihitung sebagai berikut.

Dengan demikian, persentase penduduk yang berada pada usia tidak produktif adalah sekitar 33,58%.

Jadi, jawaban yang benar adalah C.

Pernyataan yang bernilai BENAR adalah Persentase keberhasilan akun C lebih kecil dari akun D dan Persentase keberhasilan akun E bukanlah yang paling besar.

Pembahasan:

Kita dapat menggunakan rumus peluang empiris untuk mencari empat akun dengan peluang keberhasilan tertinggi. Peluang empiris dapat dinotasikan dengan rumus berikut ini.

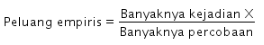
Berdasarkan rumus tersebut, kita perlu menghitung peluang keberhasilan akun dalam pembelian tiket konser dengan membandingkan antara banyaknya transaksi pembelian tiket yang berhasil dengan banyaknya transaksi yang dilakukan. Jika dilakukan perhitungan terhadap dua besaran tersebut, akan diperoleh hasil seperti pada tabel berikut.

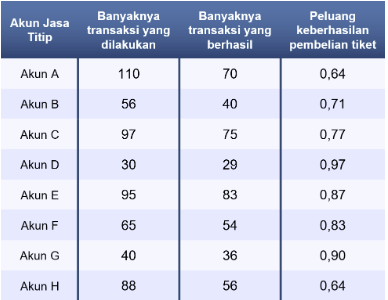
Kemudian, akan diperiksa setiap pernyataan yang ada di pilihan jawaban sebagai berikut.

Persentase keberhasilan akun A lebih besar dari akun B.

Dari tabel tersebut diperoleh persentase keberhasilan akun A lebih kecil dari akun B. Oleh karena itu, pernyataan bernilai SALAH.

Persentase keberhasilan akun C lebih kecil dari akun D.

Dari tabel tersebut diperoleh persentase keberhasilan akun C lebih kecil dari akun D. Oleh karena itu, pernyataan bernilai BENAR.

Persentase keberhasilan akun E lebih kecil dari akun F.

Dari tabel tersebut diperoleh persentase keberhasilan akun E lebih besar dari akun F. Oleh karena itu, pernyataan bernilai SALAH.

Persentase keberhasilan akun E bukanlah yang paling besar.

Dari tabel tersebut diperoleh persentase keberhasilan paling besar adalah akun D sehingga persentase keberhasilan akun E bukanlah yang paling besar. Oleh karena itu, pernyataan bernilai BENAR.

Persentase keberhasilan akun D adalah yang paling kecil.

Dari tabel tersebut diperoleh persentase keberhasilan paling kecil adalah akun A dan akun H. Oleh karena itu, pernyataan bernilai SALAH.

Jadi, jawaban yang benar adalah B dan D.

Pembahasan:

Pola susunan kursi pada gedung teater tersebut dapat diuraikan sebagai berikut.

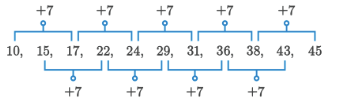
Berdasarkan pola tersebut, dapat disimpulkan bahwa banyaknya kursi yang berada pada baris kedua dari belakang atau baris kesepuluh adalah 43 kursi.

Jadi, jawaban yang tepat adalah D.

Pembahasan:

Diketahui seluruh siswa duduk tepat di satu kursi dan tidak ada kursi yang kosong pada dua baris paling akhir. Artinya, banyaknya siswa SMA yang menonton pertunjukan tersebut sama dengan banyaknya kursi pada dua baris paling akhir.

Pola susunan kursi pada gedung teater tersebut dapat diuraikan sebagai berikut.

Berdasarkan pola tersebut, dapat disimpulkan bahwa jumlah kursi yang terdapat pada dua baris terakhir, yaitu baris ke-10 dan ke-11 adalah 43 dan 45. Oleh karena itu, total banyaknya kursi yang terdapat pada dua baris paling akhir tersebut adalah 43 + 45 = 88 kursi. Dengan demikian, banyaknya siswa SMA yang menonton pertunjukan tersebut adalah 88 siswa.

Jadi, jawaban yang tepat adalah E.

Pembahasan: 

Pola susunan kursi pada gedung teater tersebut dapat diuraikan sebagai berikut.

Berdasarkan pola tersebut, dapat diketahui beberapa informasi berikut ini.

• Total kursi yang terdapat pada gedung teater adalah sebagai berikut.

Total kursi = 10 + 15 + 17 + 22 + 24 + 29 + 31 + 36 + 38 + 43 + 45

                  = 310

• Jika hanya setengah dari kapasitas gedung yang terisi, maka banyaknya kursi yang kosong adalah sebagai berikut.

Banyaknya kursi kosong  = 1/2  x  310

                                         = 155

Dengan demikian, banyaknya kursi yang kosong adalah 155 kursi.

Jadi, jawaban yang tepat adalah C.

Pembahasan: 

Misalkan X menyatakan besar gaji karyawan B.

Diketahui premi asuransi karyawan A sama dengan karyawan B. Oleh karena itu, didapat perhitungan sebagai berikut.

Premi asuransi karyawan A = Premi asuransi karyawan B

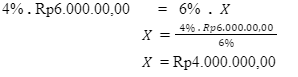
Dengan demikian, besarnya gaji karyawan B adalah Rp4.000.000,00

Jadi, jawaban yang tepat adalah D.

Pembahasan: 

Untuk menjawab soal ini, akan ditentukan terlebih dahulu gaji karyawan B serta besar premi asuransi yang harus dibayarkan oleh karyawan A maupun karyawan B.

Perhatikan beberapa perhitungan berikut.

• Besar gaji karyawan B

Misalkan X menyatakan besar gaji karyawan B. Diketahui premi asuransi karyawan A sama dengan karyawan B. Oleh karena itu, didapat perhitungan sebagai berikut.

Premi asuransi karyawan A  =   Premi asuransi karyawan B

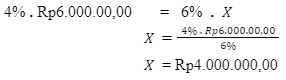
• Besar premi yang harus dibayar oleh karyawan A dan B

Besar premi = Persentase premi asuransi karyawan A gaji karyawan A

                     = 4% x Rp6.000.00,00

                     = Rp240.000,00

Akibatnya, premi asuransi karyawan B juga sebesar Rp240.000,00.

Selanjutnya, akan dianalisis pada setiap pernyataan pada pilihan jawaban yang diberikan.

• Pilihan A: Sisa gaji karyawan A setelah dipotong premi asuransi adalah Rp5.670.000,00. Sisa gaji karyawan A setelah dipotong premi asuransi dapat dihitung sebagai berikut.

         Sisa gaji karyawan A = Gaji karyawan A – Premi asuransi karyawan A

                                            = Rp6.000.000,00 – Rp240.000,00

                                            = Rp5.760.000,00

         Oleh karena itu, pernyataan pada pilihan A tidak tepat.

• Pilihan B: Sisa gaji karyawan B setelah dipotong premi asuransi adalah Rp3.870.000,00. Sisa gaji karyawan B setelah dipotong premi asuransi dapat dihitung sebagai berikut.Sisa gaji karyawan B = Gaji karyawan B – Besar premi asuransi 

                                            = Rp4.0000.000,00 – Rp240.000,00

                                            = Rp3.760.000,00

         Oleh karena itu, pernyataan pada pilihan B tidak tepat.

• Pilihan C: Premi asuransi karyawan A dan karyawan B masing-masing adalah Rp230.000,00.Telah didapatkan pada perhitungan sebelumnya bahwa premi asuransi karyawan A dan karyawan B masing-masing adalah Rp240.000,00.

         Oleh karena itu, pernyataan pada pilihan C tidak tepat.

• Pilihan D: Total gaji karyawan A dan B setelah dipotong premi asuransi adalah Rp9.520.000,00.Total gaji karyawan A dan B setelah dipotong premi asuransi dapat dihitung dengan menjumlah sisa gaji kedua karyawan tersebut setelah dipotong premi asuransi, yakni sebagai berikut.

         Total gaji = Sisa gaji karyawan A + Sisa gaji karyawan B

                         = Rp5.760.000,00 + Rp3.760.000,00

                         = Rp9.520.000,00.

         Oleh karena itu, pernyataan pada pilihan D tepat.

• Pilihan E: Selisih gaji karyawan A dan B sebelum dipotong premi asuransi adalah Rp1.500.000,00.Selisih gaji karyawan A dan B sebelum dipotong premi asuransi dapat dihitung sebagai berikut.Gaji karyawan A – Gaji karyawan B = Rp6.000.000,00 – Rp4.000.000,00

         = Rp2.000.000,00

         Oleh karena itu, pernyataan pada pilihan E tidak tepat.

Jadi, jawaban yang tepat adalah D.

Kepadatan penduduk merupakan hasil bagi antara jumlah penduduk terhadap luas wilayah.

Dengan demikian, didapatkan rumus sebagai berikut.

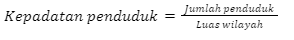
Untuk menjawab soal ini, akan dihitung kepadatan penduduk pada tiap provinsi dengan menggunakan rumus di atas.

Kalimantan Utara

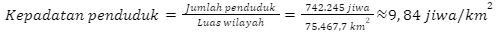
Kalimantan Barat

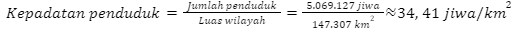
Kalimantan Timur

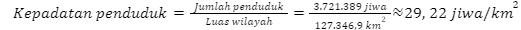
Kalimantan Selatan

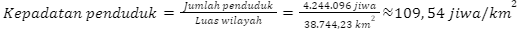
Kalimantan Tengah

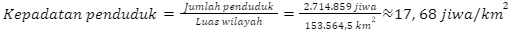
Berdasarkan hasil perhitungan tersebut, dapat disimpulkan bahwa Provinsi di Pulau Kalimantan yang memiliki kepadatan penduduk paling rendah adalah Kalimantan Utara. Dengan kata lain, provinsi di Pulau Kalimantan yang akan diprioritaskan untuk menjadi tujuan transmigrasi adalah Kalimantan Utara.

Jadi, jawaban yang tepat adalah A.

Pembahasan: 

Diketahui:

durasi film = 1 jam 25 menit 15 detik

durasi film = 5.115 detik

laju cetak = 20.000 data/detik

1 data = 48 bit

1 byte = 8 bit

Kapasitas penyimpanan yang terpakai dapat diketahui dengan perhitungan berikut ini.

= durasi film x laju cetak x jumlah bit per data

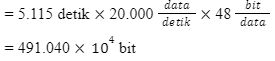
Ubah menjadi satuan byte.

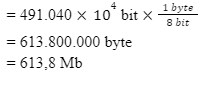
Berdasarkan hasil perhitungan tersebut, dapat diketahui bahwa kapasitas penyimpanan yang terpakai pada CD adalah 613,8 Mb.

Jadi, jawaban yang tepat adalah B.

Pembahasan:

Diketahui:

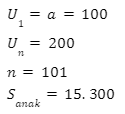
Soal ini dapat dijawab menggunakan rumus jumlah n data pada deret aritmetika berikut ini.

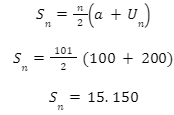
Selisih hasil hitungan Nada dan hasil hitungan dengan rumus adalah sebagai berikut.

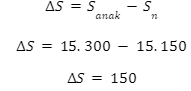
Hasil hitungan Nada lebih besar dibandingkan hasil hitungan dengan rumus, hal ini menandakan bahwa ada halaman yang terhitung dua kali oleh Nada. Hal ini dikarenakan Nada mulai menghitung dari halaman 100 sampai 200. Halaman yang terhitung dua kali oleh Nada adalah halaman 150 sehingga pernyataan A tepat. Berdasarkan hasil perhitungan tersebut, kita juga dapat mengetahui beberapa informasi lainnya

• Pernyataan B tidak tepat, karena halaman 50 tidak ikut dihitung oleh Nada.
• Pernyataan C tidak tepat, karena hasil hitungan Nada tidak sesuai dengan hasil hitungan dengan rumus jumlah n suku pertama deret pertama.
• Pernyataan D tidak tepat, karena hasil hitungan Nada lebih besar sehingga ada halaman yang terhitung dua kali, bukan tidak terhitung.
• Pernyataan E tidak tepat, karena hasil hitungan Nada lebih besar sehingga ada halaman yang terhitung dua kali, bukan tidak terhitung. Kemudian, halaman 50 tidak ada dalam rentang halaman yang dihitung Nada.

Jadi, jawaban yang tepat adalah A.

Pembahasan: 

Misalkan
Harga beras = x

Harga minyak goreng = y

Persamaan yang dibuat berdasarkan ilustrasi tersebut adalah sebagai berikut.

20x + 6y= Rp3.600.000,00

15x + 5y= Rp2.800.000,00

Kemudian, eliminasi kedua persamaan tersebut sebagai berikut.

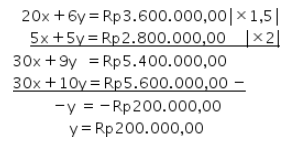
Substitusikan nilai y ke salah satu persamaan, seperti berikut.

Jadi, harga beras per karung Rp120.000,00 dan minyak goreng Rp200.000,00/dus. Total pengeluaran Pak Abdul untuk 45 karung beras dan 15 dus minyak goreng dapat dihitung sebagai berikut.

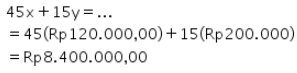
Berdasarkan hasil perhitungan tersebut, dapat diketahui bahwa total pengeluaran Pak Abdul untuk 45 karung beras dan 15 dus minyak goreng adalah Rp8.400.000,00.

Jadi, jawaban yang tepat adalah B.

Pembahasan:

Misalkan banyak siswa laki-laki di kelompok tersebut adalah x dan banyak siswa perempuan di kelompok tersebut adalah y.

Diketahui banyak teman perempuan Tari di kelompok belajar tersebut satu lebihnya dari banyak siswa laki-laki. Oleh karena itu, dapat dibuat persamaan sebagai berikut.

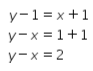
Dengan demikian, selisih banyaknya siswa laki-laki dan perempuan di kelompok belajar tersebut adalah 2 siswa.

Jadi, jawaban yang tepat adalah C.

Pembahasan:

Misalkan banyak siswa laki-laki di kelompok tersebut adalah x dan banyak siswa perempuan di kelompok tersebut adalah y.

Diketahui banyak teman laki-laki Edo di kelompok belajar tersebut sama dengan setengah dari banyak siswa perempuan. Artinya, dapat dibuat persamaan berikut.

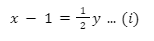
Kemudian, diketahui banyak teman perempuan Tari di kelompok belajar tersebut satu lebihnya dari banyak siswa laki-laki. Artinya, dapat dibuat persamaan berikut.

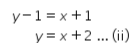
Substitusikan persamaan ii ke persamaan i sehingga didapat nilai x sebagai berikut.

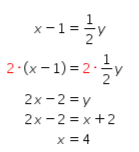
Substitusikan nilai x = 4 ke persamaan ii sehingga didapat nilai y sebagai berikut.

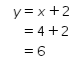
Didapat bahwa banyak siswa laki-laki dan perempuan di kelompok belajar tersebut secara berurutan  adalah 4 dan 6.

Dengan demikian, jumlah seluruh siswa di kelompok belajar tersebut adalah 4 + 6 = 10 siswa.

Jadi, jawaban yang tepat adalah E.

Pembahasan:

Berdasarkan informasi pada soal, disebutkan bahwa kondisinya adalah sebagai berikut.

Hari Minggu, maka harga tiket anak-anak Rp35.000,00 dan dewasa Rp50.000,00.

Setengah kabin (18 kabin) diisi anak-anak = tidak boleh ada kabin yang hanya diisi anak-anak, maka harus ada orang dewasa. Karena yang ditanyakan adalah pendapatan maksimum, maka digunakan asumsi sejumlah 18 kabin diisi 1 dewasa dan 2 anak-anak.

Seluruh kabin tidak ada yang kosong, maka 18 kabin sisanya diisi oleh 2 orang dewasa.

Pendapatan maksimum yang mungkin diperoleh dapat diketahui dengan perhitungan berikut

Berdasarkan hasil perhitungan tersebut, dapat diketahui bahwa jumlah pendapatan maksimum taman hiburan dari bianglala yang mungkin diperoleh pada saat itu adalah Rp3.960.000,00.

Jadi, jawaban yang tepat adalah E.