Pembahasan Soal Pengetahuan Kuantitatif

Perhatikan Diagram Venn berikut!

Misalkan himpunan A, B, dan C berturut-turut adalah himpunan siswa yang menyukai basket, renang, dan kasti di sebuah sekolah dengan total murid sebanyak 135 orang. Selain itu, diketahui pula x + y + z = p.

Dari Diagram Venn, diperoleh hubungan sebagai berikut.

Diperoleh bahwa banyak siswa yang menyukai ketiga olahraga adalah 10.

Selanjutnya, akan ditentukan nilai kebenaran dari setiap pilihan satu per satu.

Pilihan 1: Banyaknya murid yang menyukai basket, renang, dan kasti adalah 10 orang.

Seperti pada perhitungan sebelumnya, diperoleh bahwa banyak siswa yang menyukai ketiga olahraga (basket, renang, dan kasti) adalah 10.

Oleh karena itu, pilihan 1 bernilai BENAR.

Pilihan 2: Banyaknya murid yang hanya menyukai basket dan renang adalah x − 10 orang.

Banyak murid yang hanya menyukai basket dan renang adalah n(A ∩ B) − n(A ∩ B ∩ C) = x − 10..

Oleh karena itu, pilihan 2 bernilai BENAR.

Pilihan 3: Banyaknya murid yang menyukai renang atau kasti adalah 75 orang.

Banyak murid yang menyukai renang adalah 30 dan banyak murid yang menyukai kasti adalah 45, maka banyak murid yang menyukai renang atau kasti adalah 75 orang.

Oleh karena itu, pilihan 3 bernilai BENAR.

Pilihan 4: Banyaknya murid yang menyukai tepat dua jenis olahraga adalah x + y + z orang.

Perhatikan perhitungan berikut!

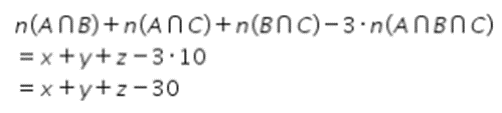
Oleh karena itu, pilihan 4 bernilai SALAH.

Dengan demikian, dapat disimpulkan bahwa pernyataan 1, 2, dan 3 SAJA yang benar.

Jadi, jawaban yang tepat adalah A.

2. Diketahui 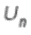merupakan suku ke-n dari suatu barisan geometri dengan tiga suku pertamanya berturut-turut adalah 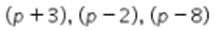. Lalu, ditanyakan suku kelima dari barisan tersebut.

Untuk menentukan suku kelima barisan tersebut, terdapat beberapa langkah yang diperlukan seperti di bawah ini.

Langkah Pertama: Tentukan nilai dari p.

Diketahui tiga suku pertama suatu barisan geometri adalah .Ingat bahwa rasio pada barisan geometri dapat ditentukan sebagai berikut.

Oleh karena itu, diperoleh hubungan sebagai berikut.

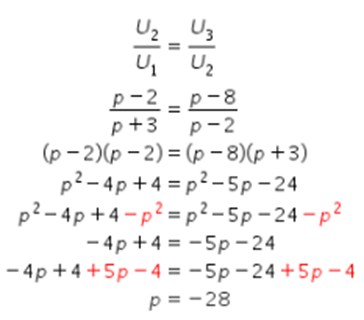
Berdasarkan perhitungan di atas, diperoleh nilai .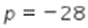

Langkah Kedua: Tentukan suku kelima barisan tersebut.

Berdasarkan nilai p yang sudah didapat, maka tiga suku pertama dari barisan tersebut adalah sebagai berikut.

Lalu, diperoleh suku pertamanya adalah dan rasionya adalah Oleh karena itu, suku kelima barisan tersebut dapat ditentukan sebagai berikut.

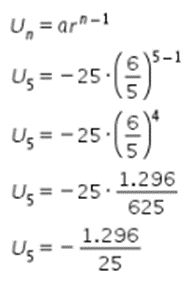
Dengan demikian, suku kelima dari barisan geometri tersebut adalah 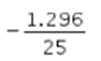. Jadi jawabannya adalah B.

3. Ingat bahwa gradien dari garis dengan persamaan 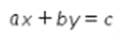adalah .Diketahui persamaan garis g ada .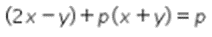

Perhatikan persamaan berikut!

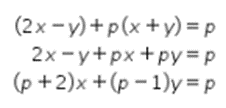
Dari bentuk tersebut, didapat bahwa gradien garis g adalah .

Kemudian, diketahui persamaan garis h adalah .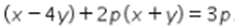

Perhatikan persamaan berikut!

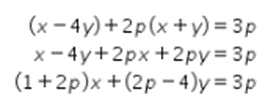
Dari bentuk tersebut, didapat bahwa gradien garis h adalah .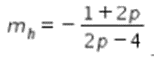

Karena garis g dan h saling sejajar, maka diperoleh hubungan sebagai berikut.

Berdasarkan perhitungan di atas, diperoleh p = 7.

Dengan demikian, nilai dari -2p adalah (-2).7 = -14.

Jadi, jawaban yang tepat adalah D.

4.  Dalam soal tersebut terdapat empat pernyataan yang diuji kebenarannya. Pilihan 1 salah karena jumlah cara duduk 7 orang secara melingkar adalah (7-1)! = 720, bukan 210. Pilihan 2 juga salah karena jika 5 soal pertama wajib dikerjakan, maka calon karyawan tinggal memilih 3 dari 7 soal yang tersisa, yaitu C(7,3) = 35 cara, bukan 120. Pilihan 3 pun salah karena kombinasi memilih 3 dari 7 orang adalah C(7,3) = 35, bukan 70. Hanya pilihan 4 yang benar, yaitu kombinasi memilih 1 pria dari 3 (C(3,1) = 3) dan 2 wanita dari 4 (C(4,2) = 6), sehingga total kombinasi 3 × 6 = 18. Jadi, hanya pernyataan keempat yang benar dan jawaban yang tepat adalah D.

5. Perhatikan perhitungan berikut!

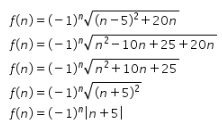
Selanjutnya, akan diperiksa tiap pernyataan yang ada.

Pilihan 1: Jika n adalah bilangan genap,  bernilai ganjil.

Jika n bilangan genap,  juga akan bernilai genap. Oleh karena itu,  juga akan bernilai genap. Artinya, untuk suatu bilangan genap , didapat perhitungan sebagai berikut.

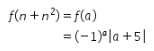
Karena a genap, maka a + 5  akan bernilai ganjil. Karena  pasti merupakan bilangan ganjil, maka  adalah suatu bilangan ganjil.

Dengan demikian, pilihan 1 bernilai BENAR.

Pilihan 2: Jika n adalah bilangan ganjil,  bernilai ganjil.

Jika n adalah bilangan ganjil, n + 5 akan bernilai genap. Karena  pasti merupakan bilangan ganjil, maka  adalah suatu bilangan genap. Dengan demikian, f(n) adalah suatu bilangan genap.

Kemudian, jika n adalah bilangan ganjil, 2n adalah bilangan genap.

Akibatnya, 2n + 5 akan bernilai ganjil. Oleh karena itu,  adalah suatu bilangan ganjil. Dengan demikian, f(2n) adalah suatu bilangan ganjil.

Karena f(n) adalah suatu bilangan genap dan f(2n) adalah suatu bilangan ganjil, maka diperoleh bahwa  adalah bilangan ganjil.

Dengan demikian, pilihan 2 bernilai BENAR.

Pilihan 3: 

Hasil dari  dapat ditentukan sebagai berikut.

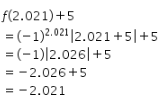
Selanjutnya, hasil dari  dapat ditentukan sebagai berikut.

Karena didapat hasil dari  dan  yang sama, yaitu -2.021, maka .

Dengan demikian, pilihan 3 bernilai BENAR.

Pilihan 4: 

Hasil dari  dapat ditentukan sebagai berikut.

Karena diperoleh , maka pernyataan 4 bernilai BENAR.

Jadi, jawaban yang tepat adalah E.

6.

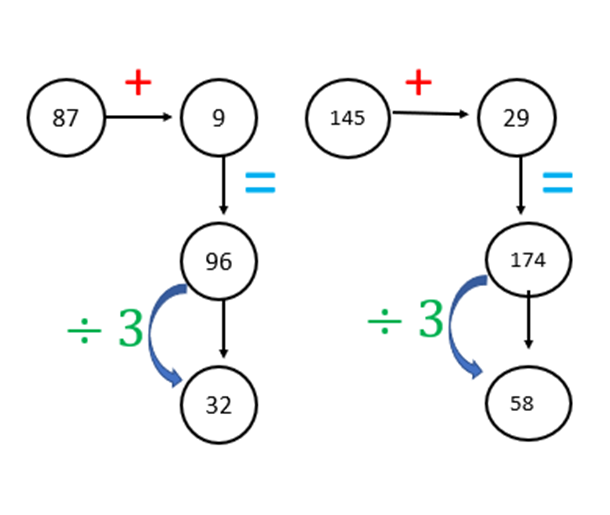
7. Perhatikan penyelesaian gambar yang pertama.

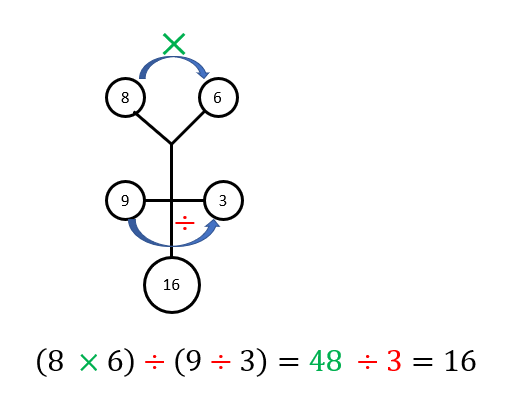
Terapkan langkah penyelesaian dari gambar pertama pada gambar kedua.

8.

9. Misalkan, banyak pekerja = x.

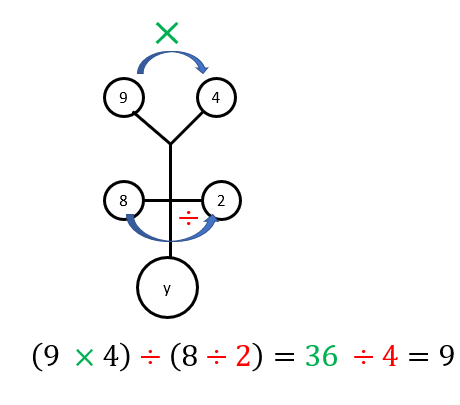
Diketahui:

Banyak pekerjaan di 5 hari terakhir adalah 500 pekerjaan.

 

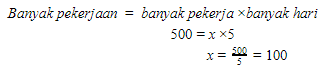
Banyak pekerja di 5 hari terakhir adalah 100 orang dan yang sudah ada adalah 60 orang.

Jadi, banyak pekerja yang harus ditambah adalah 40 orang.

10. Misalkan:

• Umur ayah = x
• Umur ibu = y
• Umur kakak = z

Rata-rata umur ayah, ibu, dan kakak 4 tahun yang lalu = 34 tahun.

 

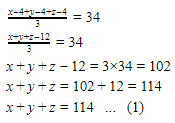
Rata-rata umur ayah dan kakak 3 tahun yang lalu = 32 tahun.

 

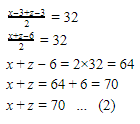
Dari persamaan (1) dan (2) didapatkan:

 

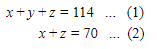
Nilai x + z = 70 substitusikan ke persamaan (1):

 

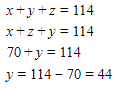
y adalah umur ibu, jadi umur ibu adalah 44 tahun.

Kemudian, lihat tabel:

P = 44 tahun

Q = 45 tahun

Nilai Q > P.

Jadi, pilihan yang tepat adalah B.

11. Perhatikan gambar!

 

a + b + c = 180^o, r = a (karena saling bertolak belakang).

 

Pernyataan (1)

 

a + c = 85^o

 

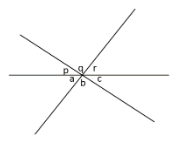
Oleh karena itu, didapat

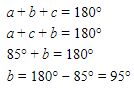
Karena besar r = a, dan nilai a belum dapat diketahui nilainya, maka pertanyaan tidak dapat dijawab hanya dengan pernyataan (1).

Pernyataan (2)

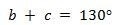
Oleh karena itu, didapat

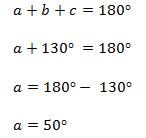
Karena besar r = a, maka didapat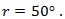 

Oleh karena itu, pertanyaan dapat dijawab hanya dengan pernyataan (2).

Jadi, pernyataan (2) saja cukup untuk menjawab pertanyaan, tapi pernyataan (1) saja tidak cukup.

 

12.  Dari soal, diketahui kebun berbentuk lingkaran dan jarak antar pohon adalah 2 meter.

Ditanyakan: banyak pohon yang dibutuhkan untuk ditanam di sekeliling kebun.

Untuk menentukan banyak pohon yang dibutuhkan untuk ditanam, yang perlu diketahui adalah kelilingnya.

Pernyataan (1)

Luas kebun = 15.400 m²

Karena kebun berbentuk lingkaran,

 

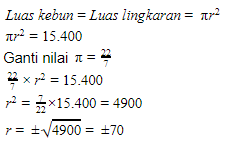
Tapi karena r adalah ukuran panjang, nilainya pasti positif. Jadi, r = 70 m.

Keliling kebun = keliling lingkaran = 2πr.

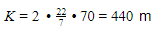
Banyak pohon yang dibutuhkan:

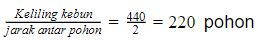
Dengan pernyataan (1) saja sudah dapat menjawab pertanyaan.

Pernyataan (2)

Keliling kebun = 440 m

Banyak pohon yang dibutuhkan:

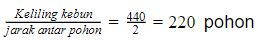
Dengan pernyataan (2) saja sudah dapat menjawab pertanyaan.

Jadi, pilihan yang tepat adalah D

13. 

Pertama, urutkan data dari tujuh bilangan. Karena x adalah median dari 7 bilangan, artinya x berada di tengah urutan.

4, 6, 12, x, 15, 18, 24

 

Nilai x yang mungkin adalah 13 dan 14. Kemudian, tentukan rata-rata dari data:

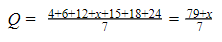
Rata-rata data jika nilai x = 13:

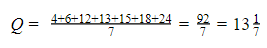
Jika x = 13, maka Q > P.

Rata-rata data jika nilai

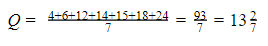
Jika x = 14, maka P > Q.

Karena tidak dapat memutuskan mana jawaban yang tepat, kesimpulannya adalah Informasi yang diberikan tidak cukup untuk memutuskan salah satu dari tiga pilihan di atas.

14. Perhatikan gambar!

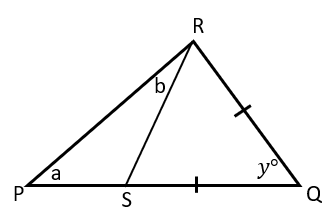
Perhatikan segitiga PRS, a = 48^o , dan b = 22^o .

Jumlah sudut pada segitiga adalah 180^o.

 

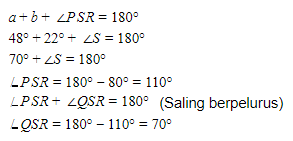
Perhatikan segitiga QRS yang merupakan segitiga sama kaki dengan QR = QS, sehingga:

 

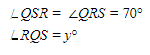
Jumlah sudut pada segitiga adalah 180^o.

15. 

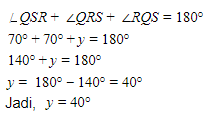
Untuk menentukan koordinat yang terletak pada garis, maka tentukan terlebih dahulu persamaan garis yang melalui titik tersebut.

Garis melalui titik (2,-1) dan mempunyai gradien m = 1/2 dapat ditentukan menggunakan persamaan:

y – y₁ = m(x – x₁)

Ganti nilai x₁, y₁, dan m dengan nilai yang diketahui dari soal, yaitu:

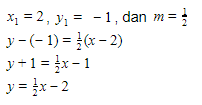
Untuk menentukan titik koordinat yang terletak pada garis dapat dilakukan dengan memasukkan koordinat yang ada pada soal ke persamaan garis yang didapat, yaitu .

(1) (0,2)

Titik (0,2) tidak terletak pada garis .

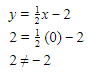
(2) (-2,0)

Titik (-2,0) tidak terletak pada garis .

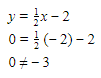
(3) (2, 1/2)

Titik (2, -1/2) tidak terletak pada garis .

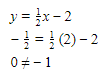
(4) (4,0)

Titik (4,0) terletak pada garis .

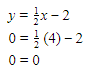
Jadi, pilihan yang tepat adalah D yaitu HANYA (4) saja yang benar.

16. Dari soal diketahui banyak kursi yang tersedia adalah 8 kursi dan hanya akan diduduki oleh 4 orang.

Banyak susunan 4 orang duduk pada kursi yang disediakan adalah P.

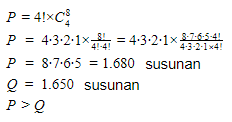
Jadi, jawaban yang tepat adalah A.

17. Dari soal diketahui ada 3 lemari.

Setiap lemari terdapat p laci.

Setiap laci terdapat 5 wadah amplop.

Setiap wadah amplop terdapat r amplop.

Jadi, di dalam 3 lemari terdapat:

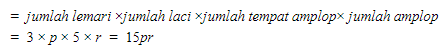
Jadi, jawaban yang tepat adalah B.

18. Dari soal diketahui:

Karyawan yang memiliki gaji Rp8.000.000,00 ada 8 orang.

Karyawan yang memiliki gaji Rp6.000.000,00 ada 10 orang.

Karyawan yang memiliki gaji Rp5.000.000,00 ada 7 orang.

Jumlah karyawan seluruhnya ada 25 orang.

Dengan menggunakan rumus rata-rata:

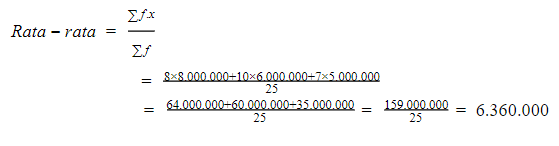
Jadi, rata-rata gaji 25 karyawan berkisar Rp6.360.000,00.

19. Untuk menentukan rata-rata dari suatu himpunan bilangan adalah dengan menjumlahkan semua data dibagi dengan banyak data.

Dari soal diketahui jumlah himpunan bilangan adalah 2.091.

Pernyataan 1 adalah Bilangan terbesar adalah 149 dan bilangan terkecil adalah 41.

Pernyataan ini tidak membantu untuk mendapatkan nilai rata-rata dari bilangan tersebut.

Pernyataan 2 adalah Anggota himpunan bilangan adalah 17.

Banyaknya anggota himpunan bilangan sama artinya dengan banyak bilangan yang terdapat dalam himpunan bilangan, sehingga dapat membantu untuk menentukan nilai rata-rata himpunan, yaitu:

 

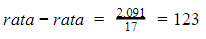
Jawaban yang tepat adalah B karena pernyataan 2 saja cukup, tetapi pernyataan 1 saja tidak cukup.

20. Untuk menentukan median dari suatu himpunan bilangan adalah dengan mengurutkan semua data dari yang terkecil sampai yang terbesar.

Dari pernyataan 1), diketahui jumlah anggota himpunan K adalah 5 bilangan bulat, tetapi tidak diketahui anggota-anggota himpunannya sehingga kita tidak dapat menentukan median dari himpunan K.

Dari pernyataan 2), yang diketahui nilai rata-rata dan nilai dari modus. Data ini tidak membantu kita dalam menentukan nilai median.

Sehingga, pernyataan 1) dan pernyataan 2) tidak cukup untuk menjawab pertanyaan